
Defining the Valid 16-bit Position Range
For general scaling information, see the Scaling Overview topic.
Because the RMC uses 16-bit positions, positions must all fit within a range of 65,536 position units. Because position units are user definable, this range does not limit most applications. See the section below on defining position units.
For MDT axes, the Offset parameter is used with the Scale parameter to define the position range. If the Scale parameter is negative, then the position range extends from the Offset value minus 65535 up to the Offset value. If the Scale parameter is non-negative, then the position range extends from the Offset value up to the Offset value plus 65535. The following chart summarizes this concept:
|
Scale |
Min. Position |
Max. Position |
|
< 0 |
Offset - 65535 |
Offset |
|
³ 0 |
Offset |
Offset + 65535 |
However, because the Offset is also used to convert transducer counts to position units, it cannot be set independently.
Translating to and from Position Units
The Scale, Offset, and the Prescale Divisor bits of the Configuration word parameters are used to define position units as a function of transducer counts. Below is shown an example MDT and the effect of the Scale, Offset, Extend and Retract Limits:

The following formula summarizes the translation from transducer counts to Actual Position units:
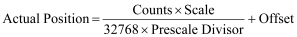
If the Actual Position overflows the valid 16-bit position range, as described above, the Position Overflow bit will turn on, forcing the axis to halt.
There are two main ways to calculate the Scale, Offset, and Prescale Divisor bits. Each method is described below. Notice that both have automatic Calibration Utilities built into RMCWin. It is recommended that these be used, but the underlying math is described below.
Method 1: P0/P1 Calculation
The simplest way is the physically measure the axis’s position at two points and read how many counts the RMC reports at each position. If we call the two positions, in user position units, P0 and P1, and call the corresponding counts C0 and C1, the following two equations will give a Scale and Offset. Notice that the Prescale Divisor is left out at this point; it is assumed to be 1:
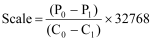
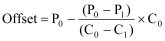
Once the Scale is calculated, the Prescale Divisor can be calculated. The Prescale Divisor can have values of 1, 2, 4, or 8. Because the Scale is always divided by the Prescale Divisor, you essentially have a fractional scale. Pick the largest Prescale Divisor you can multiply the Scale by and still be between 32768 and 32768. For example, suppose your Scale comes to 6324.70. The following table shows the possible Scales and Prescale Divisors you could use and the effective scale:
|
Scale |
Divisor |
Effective Scale |
Error from 6324.70 |
|
6325 |
1 |
6325/1 = 6325 |
0.005% |
|
12649 |
2 |
12649/2 = 6324.5 |
0.003% |
|
25299 |
4 |
25299/4 = 6324.75 |
0.0008% |
|
50598 |
8 |
Invalid scale |
Invalid |
Therefore, in this example, a Scale of 25299 and a Prescale Divisor of 4 should be used. If the Scale you calculate comes to 32768, enter 0 instead.
These calculations can be done automatically using the Position Scale/Offset Calibration Utility feature in RMCWin.
Method 2: Using the MDT Calibration Number
The Scale can also be calculated using the MDT calibration number (nominally 9.012 microseconds per inch) with the following formula. Notice that the Prescale Divisor is left out at this point; it is calculated after the initial Scale value has been calculated, as described in Method 1:
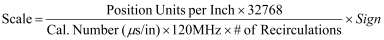
In the above formula, the 120MHz comes from the RMC’s internal counter, and Sign equals +1 when an extend move yields increasing Actual Position counts, and -1 when an extend move yields decreasing Actual Position counts. The calibration number must be specified in the same units as the Position Units (inches, mm, etc.). Position Units are generally 0.001 inches or 0.1 mm. Usually there are 1000 Position Units per inch when the calibration number is in microseconds per inch.
Once the Scale and Prescale Divisor have been calculated, the Offset can be calculated:
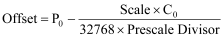
These calculations are done automatically using the MDT Scale/Offset Calibration Utility feature in RMCWin.
Example 1
A system has an MDT with a calibration number of 9.1392 ms per inch and 1 recirculation. The desired position units are thousandths of an inch. Therefore, there are 1000 position units per inch. At the desired 0 position, the MDT produces 425 counts.
We first calculate the exact Scale:
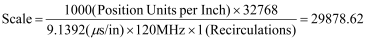
With the exact Scale value, we must choose the Prescale Divisor and the rounded Scale value. The highest divisor value we can use is 1; multiplying the scale by 2, 4, or 8 would all overflow the Scale limits of ±32767. Therefore we have the following parameters:
Scale = 29879
Prescale Divisor = 1
Next, we must calculate the offset:
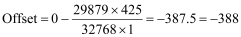
Example 2
A system has an MDT with a calibration number of 9.0108 ms per inch and 1 recirculation. The desired position units are tenths of a millimeter. At the desired 0 position, the MDT produces 1122 counts.
We must first calculate the scale, but in order to do that we need to know how many position units there are in an inch:
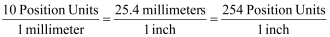
So, we now calculate the exact Scale:
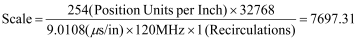
With the exact Scale value, we must choose the Prescale Divisor and the rounded Scale value. The highest divisor value we can use is 4; multiplying the scale by 8 would overflow the Scale limits of ±32767. Multiplying the exact scale by this divisor value and rounding gives us the following parameters:
Scale = 30789
Prescale Divisor = 4
Next, we must calculate the offset:
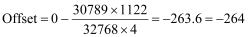
Example 3
A system has an MDT with a calibration number of 8.9772 ms per inch and 8 recirculations. The desired position units are thousandths of an inch. Therefore, there are a thousand position units per inch. At the desired 0 position, the MDT produces 28226 counts.
We begin by calculating the exact Scale:
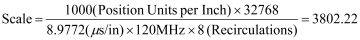
With the exact Scale value, we must choose the Prescale Divisor and the rounded Scale value. The highest divisor value we can use is 8. Multiplying the exact scale by this divisor value and rounding gives us the following parameters:
Scale = 30418
Prescale Divisor = 8
Next, we must calculate the offset:
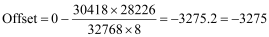
Copyright (c) 1997-2015 by Delta Computer Systems, Inc.