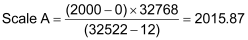
Example 1
Suppose a pressure transducer gives an output from 0 to 10 volts. This range is represented by Counts A from 0 to 32500. Also suppose that the range of pressures which will be used are from 0 psi to 2000 psi, and 0 psi gave a reading of 12 counts and 2000 psi gave a reading of 32522 counts.
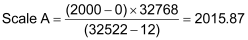
Since the scale is less than 16383.5, use the Prescale Divisor bits in the Configuration Word to divide the transducer counts by 8. Then multiply the scale by 8 to obtain:
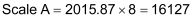
This gives us an effective scale of 16127/8 or 2015.875, which is closer than we would have been if we did not use the Prescale Divisor and instead used a scale of 2016.
An alternative way of doing this without actually measuring the pressure independently is to trust the gauge. That is, assume that 0 psi will give 0 counts, and 2000 psi will give 32,500 counts. Using these numbers, we get the following equation:
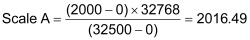
Again, we will apply a Prescale Divisor of 8 to obtain:
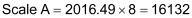
Next, we must calculate the offset. We use the following equation:
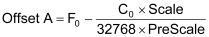
Therefore, by using the first point (0 psi at 0 counts or 0mV) and the second method of calculating the scale, we get the following:
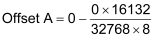
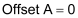
As you can see, the offset for gauges that give 0 volts at 0 pressure units will always have 0 for an offset.
Example 2
Suppose a pressure transducer gives an output from 4 to 20mA. This range is represented by Counts from 6500 to 32500. Also suppose that the range of pressures which will be used are from 0 to 10 bars, and 0.0 bars read 6487 counts and 10.0 bars read 32662 counts. We must choose our position units first. It is not a good idea to just use bars, as the user will only be able to see 0 to 10 bars and no fractions. Therefore, it makes more sense to use millibars as position units and go from 0 to 10,000 millibars. The scale calculation goes as follows:

Again, since the scale is less than 16383.5, use the Prescale Divisor bits in the Configuration Word to divide the transducer counts by 2. Then multiply the scale by 2 to obtain:

Assuming we cannot or do not want to verify the gauge’s accuracy, we can use the specified gauge requirements. Therefore, we assume that 0.0 bars reads 6500 counts, and 10.0 bars reads 32500 counts. Using these numbers, we get the following equation:
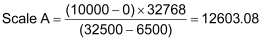
Again, we will apply a Prescale Divisor of 2 to obtain:
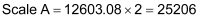
Next, we must calculate the offset. We use the following equation:
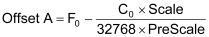
Therefore, by using the first point (0 psi at 6500 counts or 4mA) and the second method of calculating the scale, we get the following:
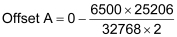
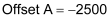
Example 3
Suppose we want to control differential force. We use the same gauges on both the A and B sides of the cylinder. These gauges are rated to have 4mA at 0 psi and 20mA at 7500 psi. Therefore, each channel will have 6500 counts at 0 psi and 32500 counts at 7500 psi. The cylinder has an internal diameter of 6 inches. The rod has an outside diameter of 2 inches. Therefore we find the maximum force applied on each end:
Force = Pressure x Area
Force on A Side = Pressure x Cross Section of Cylinder
Force on A Side at 20mA = 7500 psi x ( p x 3 inches x 3 inches )
Force on A Side at 20mA = 212,057.5 pounds
Force on B Side = Pressure x ( Cross Section of Cylinder - Cross Section of Rod )
Force on B Side at 20mA = 7500 psi x ( p x 3 inches x 3 inches - p x 1 inch x 1 inch)
Force on B Side at 20mA = 188,495.6 pounds
We assume that we will use forces up to 150,000 pounds. Because the RMC is limited in force units from ±32,767, we cannot use pounds as our force units, but instead must use 10-pound units. Therefore, 150,000 pounds will be represented as 15,000 force units.
Using this assumption, can calculate the scale.
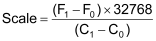
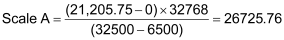
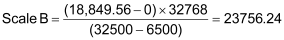
Both are above 16383.5, so our Prescale Divisor must be 1 (the Prescale Divisor bits will both be 0). Therefore, our scales are as follows:
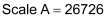
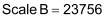
Next, we must calculate the offsets for both channels. We use the following equation:
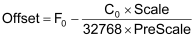
Therefore, by using the first point (0 ten-pound units at 6500 counts or 4mA) for both channels, we get the following:
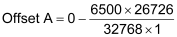
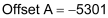

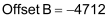
Copyright (c) 1997-2015 by Delta Computer Systems, Inc.